Как определить размеры магнитопровода дросселя импульсного преобразователя. Часть 1

Методики расчета импульсных преобразователей иногда вызывают чувство легкой паники, особенно когда дело доходит до выбора магнитопровода индуктивных элементов. Почему-то этот вопрос часто умалчивается многими производителями электронных компонентов даже с мировым именем. Например, в [1] очень подробно рассмотрены вопросы расчета обмоток дросселя, в том числе и способы уменьшения индуктивностей рассеяния – одной из основных проблем обратноходовых схем. Но выбор магнитопровода производится на уровне общих рекомендаций из таблиц, содержащих наиболее подходящие для данного случая модели. Конечно, если преобразователь работает на нужной частоте и имеет нужное выходное напряжение, то эти таблицы очень полезны. Но что делать, если параметры работы преобразователя имеют другие значения? И почему рекомендуются именно эти магнитопроводы, насколько они оптимальны? Эти вопросы в большинстве случаев остаются без ответа.

Еще большей тайной покрыта методика выбора магнитопровода в другом документе [2]. Там просто выбирается сердечник EFD30/15/9 без каких-либо комментариев и пояснений.

На сегодняшний день вопросам расчета индуктивных элементов посвящено множество публикаций. Например, очень подробно эти вопросы рассмотрены в книге [3], пережившей уже четыре переиздания. Но до сих пор выбор магнитопровода для моточных узлов импульсных преобразователей, особенно дросселей, вызывает у разработчиков ряд затруднений и чаще всего сводится к «эмпирическому» перебору доступных типоразмеров.

В данной статье, являющейся продолжением цикла посвященного импульсному преобразованию электрической энергии [4 – 8], рассмотрено, как связаны геометрические размеры магнитопровода с характеристиками преобразователя, и ключевые факторы, влияющие на эту связь. Этот материал позволит глубже понять процессы, происходящие в индуктивных элементах, и поможет в нестандартных ситуациях, часто возникающих на практике. А желающие еще глубже разобраться могут ознакомиться со статьей [9], в которой эти вопросы рассмотрены более подробно.

На какие параметры магнитопровода необходимо обращать внимание

В простейшем случае индуктивный элемент состоит из магнитопровода и обмотки (Рисунок 1). При протекании электрического тока по любому проводнику выделяется тепло со скоростью, определяемой законом Джоуля-Ленца:

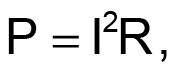(1)

где

Р – мощность тепловыделения (количество выделяемого тепла в единицу времени);
I – действующее (эффективное) значение тока;
R – сопротивление проводника.

Величина тока I определяется назначением и режимом работы индуктивного элемента. В большинстве случаев разработчик может ее рассчитать, но не изменить. Это означает, что единственным способом уменьшить количество выделяемого обмоткой тепла является уменьшение ее сопротивления R, которое рассчитывается по формуле:

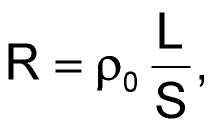(2)

где

ρ₀ – удельное сопротивление токопроводящего материала;
L – длина проводника;
S – площадь поперечного сечения.

Количество доступных материалов, обладающих низким удельным сопротивлением ρ₀, очень ограничено. Конечно, можно рекомендовать изготовить обмотку из золотого или серебряного провода, но общеизвестно, что на практике чаще всего используют медь или алюминий. Длина провода L зависит от геометрических размеров магнитопровода, который еще предстоит выбрать. Она пропорциональна количеству витков обмотки и плохо поддается изменению. Таким образом, единственным способом регулировки тепловыделения остается изменение площади поперечного сечения провода S, которая, с одной стороны, не может быть бесконечно малой, иначе провод перегреется, а с другой – не может быть бесконечно большой, потому что это ухудшит большинство остальных характеристик прибора.

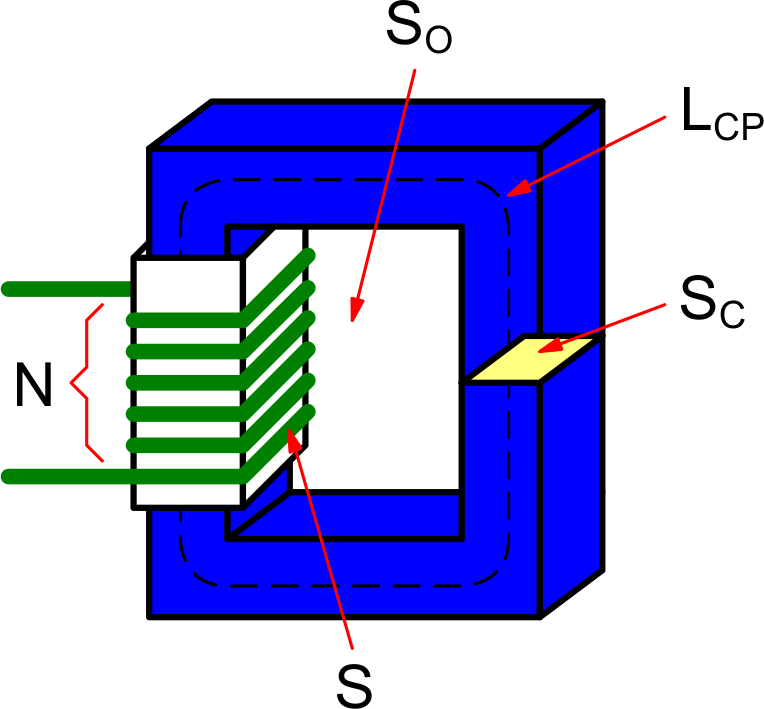
Рисунок 1.	Устройство простейшего индуктивного элемента.

Обмотки индуктивных элементов располагаются в специальном отсеке магнитопровода, называемом окном, который имеет конечные размеры, а значит и фиксированную площадь S_О. Это означает, что в окне может поместиться определенное количество витков, поэтому желательно, чтобы провод был как можно тоньше – это позволит разместить больше витков, или использовать более компактный магнитопровод с меньшим значением S_О.

На практике при расчете индуктивных элементов оценку необходимой площади сечения проводника S часто проводят по упрощенной методике:

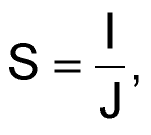(3)

где J – плотность тока в проводнике.

Допустимая плотность тока J зависит в первую очередь от условий охлаждения. При хорошем охлаждении выделение даже значительного количества тепла не приведет к перегреву индуктивного элемента, поэтому на практике J может изменяться в широких пределах – от 2 А/мм² до 10 А/мм². И хоть реальная плотность тока все равно выбирается разработчиком на основании достаточно «размытых» рекомендаций, а чаще всего – на основании собственного опыта и интуиции, такой метод уже позволяет существенно упростить процесс выбора.

Таким образом, минимально необходимая для размещения обмотки площадь окна в идеальном случае определяется формулой:

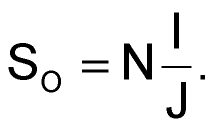(4)

Единственным неизвестным параметром в формуле (4) является количество витков N, зависящее от параметров и режима работы магнитной системы по закону Фарадея:

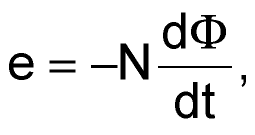(5)

где

е – ЭДС самоиндукции на выводах обмотки;
Ф – магнитный поток в магнитопроводе.

Магнитный поток Ф равен количеству линий магнитной индукции В, проходящей через некоторый замкнутый контур, поэтому:

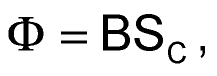(6)

где S_C – площадь поперечного сечения магнитопровода.

Если на протяжении некоторого интервала времени Δt к обмотке приложить некоторое неизменяющееся напряжение U, то, согласно (5) и (6), это приведет к изменению магнитной индукции в магнитопроводе на величину:

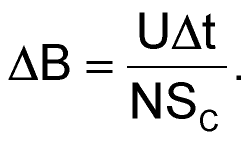(7)

Выразим из формулы (7) количество витков N и подставим его в формулу (4):

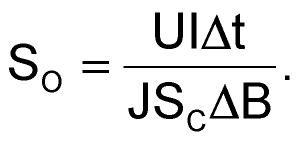(8)

Из формулы (8) видно, что площадь сечения магнитопровода S_C и необходимая площадь окна S_Oвзаимосвязаны. Так, например, если, не меняя размах магнитной индукции ΔB, увеличить площадь поперечного сечения магнитопровода в два раза, то для размещения обмотки, за счет уменьшения в два раза количества витков, потребуется окно в два раза меньшего размера.

Такая зависимость привела к тому, что для оценки требуемого размера магнитопровода используют произведение площадей сечения магнитопровода и окна S_СS_О, которое можно легко получить из формулы (8):

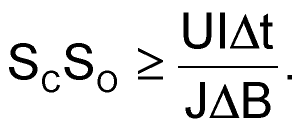(9)

Формула (9) записана в виде неравенства неслучайно, ведь все, что было сказано выше, относилось к определению минимально необходимых площадей S_C и S_O. То есть, если выбрать магнитопровод с бóльшим значением произведения S_CS_O, то прибор с большой вероятностью можно реализовать физически, а вот с меньшим уже проблематично: или обмотки не поместятся в окне, или магнитопровод войдет в насыщение из-за увеличенного значения ΔB, или провод перегреется из-за чрезмерно высокой плотности тока J.

Обратите также внимание, что размерностью числителя формулы (9) является джоуль (вольт-ампер-секунда или ватт-секунда). Это означает, что физические размеры магнитопровода прямо пропорциональны количеству энергии, проходящей через индуктивный элемент.

Максимальный размах магнитной индукции ΔВ в реальных магнитопроводах ограничен индукцией насыщения В_НАС магнитного материала и типом индуктивного элемента. Как показано в [8], для трансформаторов ΔВ может достигать величины 2В_НАС, а вот для дросселей эта величина ограничена не только индукцией насыщения, но и остаточной намагниченностью B_R (ΔВ < В_НАС – B_R). Это означает, что при том же самом уровне энергии, с которым работает индуктивный элемент, магнитопровод дросселя будет как минимум в два раза больше магнитопровода трансформатора, а, учитывая, что многие дроссели импульсных преобразователей проектируются для работы в режиме ΔВ ≈ 0.3В_НАС, становится очевидно, что в этом случае дроссель будет примерно в шесть раз больше трансформатора при тех же энергетических показателях.

Кроме того, в отличие от трансформаторов, не предназначенных для накопления энергии, магнитопровод дросселя является энергетическим хранилищем, поэтому для дросселей, кроме конструктивных ограничений S_CS_O, магнитопровод должен еще иметь определенный объем активного магнитного материала V_С ≈ S_CL_СР (L_СР – средняя длина магнитной линии). Если в трансформаторе площадь поперечного сечения магнитопровода, чисто теоретически, может быть нулевой (при бесконечной площади окна и бесконечном количестве витков обмоток), то дроссель при таких условиях работать не будет, потому что у него будет отсутствовать место для хранения энергии.

Таким образом, при выборе магнитопровода любого индуктивного элемента необходимо обращать внимание на конструктивный параметр S_CS_O, компоненты которого (S_C и S_O) всегда присутствуют в технической документации, а для дросселей еще необходимо дополнительно проверять объем магнитного материала S_CL_СР.

Список источников